Naive Compilation to BrainF--ck: a Study
Some months ago my trusty old Lenovo was going through rather heavy computations when it suddenly stopped, exhaled a small puff of blue smoke and never responded to any key press again. While its computational essence had moved to the realm of eternal primes hunt, I managed to salvage an SSD from its earthly remains. It accumulated quite a few fun projects and notes over the years which I will try to publish. I will not be editing them much since they have already seen years of sporadic improvements waiting to become perfect, so they will inevitably end up being a bit of stream-of-conciousness-y. Despite that I believe there are a couple of tricks lurking inside which are worth sharing.
revision 0.6.3
BrainF*ck (BF) is a fine specimen of Turing Tarpits: it is compact, easy to explain and seemingly easy to reason about. It is trivial to write an interpreter for it or to build a hardware machine that would use it as binary code. The only problem with the language is that it becomes exponentially harder to write more complex programs in it. The main reason for that is very repetitive, extremely mind-numbing nature of BF programs. The standard solution for dealing with repetitive, mind-numbing tasks is to employ a computer to do them. Computers work really well at translating code from a more human-friendly representation to a machine-friendly one.
In this study I’ll document my experiments with one particular approach to compilation to BF. Before I delve into details a word of
WARNING! This is not a tutorial on how to write a good compiler. Moreover, this is not exactly a tutorial on how to write any compiler. The system described in this text is suboptimal >by design<. It was developed intermittently to test several concepts and should be treated only as such: an experimental oddity.
The approach I used resulted in a not particularly handy solution, but it provided me with a number of insights on several aspects of both compiler design, implementations and BF viability as a computation model in general. I will share my observations here.
Once again, this is not how one should write a compiler. For those who want to learn good practices I prepared a list of very good books (in no particular order) at the bottom of this page. For those who like lurking in weird places – welcome! get ready for the journey.
A Brief Pre-History
The idea to compile something higher-level to BF first came to me some time around fall 2007. Back then I had rather vague idea of how exactly this could have been achieved, but considered it worth a try and made a mental note to do it someday. Then other things preempted and the idea was forgotten for some years.
Around 2009 I started diving into the mysterious world of DIY CPUs and ran into a problem of formulating my very own instruction set for a computer. I have briefly looked at BF and code generation for it, but promptly turned away from it. Then I turned away from any low-level matters for a few years.
I got my first simulated hardware BF design working some time around 2013. Now I had a problem on my hands: printing “Hello world!” is fun, but does not make a particularly impressive demo. I wanted math. I wanted trigonometry. I wanted simple simulations. Writing non-trivial math manually in plain BF is possible, but one must be courageous or desperate enough to attempt that. I was neither, so first I tried to cheat and come up with a tool that would search the space of all possible programs for those which terminate in reasonable amount of time and match desired inputs to outputs. I tried genetic algorithms for that only to realize that there are no smooth gradients present in that space, but rather sparsely distributed special points which represent useful programs and endless ocean of noise between them. I mothballed this project. (I actually revived it briefly within an attempt of building a fully reversible interpreter in Prolog, but this would take the story even further into the weeds, so maybe I’ll put the notes on it together some other day). I had no choice, but to stick with the plan of building some sort of a compiler for that, or at least some hybrid monstrosity that would short-cut the most repetitive parts for me. Here the prehistory ends and the history begins.
Intermezzo: BF refresher
A very compelling thing about BF is that it is possible to fully explain the model in under five minutes. I’ll do it right here right now to keep the text more or less self-sufficient. Feel free to skip if you are familiar with it.
BF machine consists of two sequential memory devices, one to store code, the other to store data, usually referred to as “tapes” (think of them like of VHS or compact cassettes of sorts). Both tapes start in the leftmost position and move to the left or to the right depending on their cumulative state. The data tape is normally considered circular i.e. once a tape is exhausted in either direction it implicitly rolls over to the opposing end. Data is stored as discrete 8-bit morsels referred to as cells. Data tape starts empty, i.e. initially each cell stores a zero. The machine has an unspecified device which can somehow read 8-bit wide values from a user (i.e. do input) and display cells’ contents to a user (i.e. do output). On each clock cycle a core of a machine determines whether to modify a value on data tape, or move any of the tapes basing on instructions supplied as a program. A BF program is a potentially infinite sequence consisting of eight allowed symbols written to the code tape:
+ which instructs the machine to increments current cell\'s contents
- which does the opposite to +
> tells the machine to move data tape one position to the left
< -//-//- to the right
. prints current cell to output
, reads 8 bits from input and overwrites current cell with this data
[ does nothing if current data cell is not zero, all instructions between
thi bracket and a matching ] are skipped otherwise
] does nothing if current cell is zero, data tape is rewound to a symbol right
after matching [ otherwise
Any other symbols are ignored (or are simply unrepresentable – this is an implementation detail). The original specification also put a limit on the size of data tape, but this limit is rather artificial and immaterial. BF implementations usually have an implicit ninth symbol – the end of tape. It is not usually brought up, but it is often assumed that once code tape runs out a machine halts. It is not a fundamental aspect, though, since code written for a machine with an implicit halt and with a looped program tape differs only in the way it is terminated: lack of a halt requires a few symbols of additional boilerplate to trap an interpreter in an expected state. I will assume that any referenced implementation halts on reaching end of tape and will explicitly state if I ever need to change this assumption.
There is no requirement for an input or output device to support any specific characters encoding, but often it is assumed that ASCII is used for both.
It turns out that given enough tape this small and rather unsophisticated
system is Turing complete. This also teaches us that it does not take much to
be computationally equivalent to <insert your favourite CPU here>
. Whether it is comparable from practical perspective or not we’ll learn from this text.
Writing programs in BF: the basics
Complexity of writing programs in BF is reciprocal to its simplicity. Let us briefly consider the elementary BF programming before delving into generating BF code programmatically.
Once the basics of BF are understood (in about five minutes or less) the next question is usually “Now what?”. Now it is time to get accustomed to a very different computational model.
Normally one would expect a computer to have some semi-permanent storage and some easily
acessible scratchpad area,
be it registers plus RAM¸ stack plus RAM or some similar combination. BF lacks
this and does not distinguish between storage area and scratch – the entirety
of data tape is storage area, and the entirety of it is scratch: somewhat like
a CPU with tens of thousands of registers. Furthermore, the only allowed data
manipulation type is cell modification. No data transfer instructions, no
sophisticated addressing modes. Just increment, decrement or copy from input.
How one could do anything at all with such a model? The secret ingredient that
is actually the workhorse of the model is this pair of instructions: []. It allows
to conditionally execute or skip pieces of code. Turns out, that with enough
patience it is possible to build the plethora of more familiar abstractions just from
these two.
Let’s have a look at how this could be done.
Consider the following program: +. It is not very useful, but is very
straightforward: when a BF machine powers up and executes it it increments the
contents of the first data cell once and finishes. Now consider what happens
when I enclose + in brackets: [+]. When an interpreters powers up its current
cell is the leftmost cell, which is empty, as all other cells are. The first
instruction is [ which tells the interpreter to skip everything until a
matching ] is found if current cell is empty. But we already know that the
current cell is empty, so we can construe that every instruction until matching
] will be skipped. In the program above there is precisely one instruction
to be skipped followed by a ] followed by implicit end of tape. Thus this
program is nothing more than a fancy way of doing nothing.
Now suppose we do want to do something. Consider the following program: +[-].
First we increment the current cell. Then we enter the brackets (because current cell
is not empty anymore), then we decrement the current cell, then we exit the brackets
because at the moment the interpreter reached the closing bracket the current cell
is empty. The tape ends here. Still nothing is done but now with even more style!
What would happen if the first + were duplicated? Like this: ++[-].
Well, it is obvious that first two steps would set the leftmost cell to 2, then
the brackets would be entered, then current cell would be decremented by 1 leaving
it with value 1. Thus the interpreter would arrive at closing bracket with a non-empty
current cell. By definition this requires the interpreter to rewind program tape to
the symbol right after the matching bracket. In this example there is no nesting and
effectively no code between brackets, so this would mean that the interpreter would
have to process - again. Which, in turn, would set the current cell to zero and break the
loop. ([-] is an important BF idiom used to unconditionally clean the current
cell).
What else could be done easily? Turns out, that copying cells and multiplying cells
by a fixed and known amount is rather easy. Consider this snippet: +[>++<-].
Here we first make sure that the first cell is not empty and contains exactly 1.
Then we enter the loop, move data tape one cell to the left with >
which means that current cell is now cell No.2, then we increment the current
cell twice (which results in 2 being stored in cell No.2 which is now the
current one), then we move data tape to the right with < which makes
cell No.1 current and decrement the current cell. Since on entering the loop cell
No.1 contained 1 it contains 0 now and the loop is broken. It is not hard to imagine
how this approach could be scaled: the first cell could be set to some number
other than 1, the second cell could be incremented by some number other than 2,
or it could be third or n-th cell instead. Moreover, these variations could be
combined: ++[>++>+++<<-]. In the last example I set the first cell to 2, then
enter the loop, move tape to the left, increment current cell twice, move the tape
to the left again, increment the current cell (now cell No.3) thrice, then move
the tape to the right two times and decrement the current cell. It is clear that
after a machine halts there will be 4 in cell No.2 and 6 in cell No.3. (It is also
trivial to see that a program +[] would never terminate. This is one of the
ways to mark the final state of a program for an interpreter with a looped program
tape).
The last trivial program in BF I believe is worth considering is this:
++[>+>+<<-]>>[<<+>>-]. This code duplicates a cell to some other cell
(in this case to its right neighbor). Remember, that there is no copy operator
in BF, only destructive cells manipulations, so if one needs to copy some data
they would need to build something that does enough destructive operations to
maintain an illusion of a non-destructive process. This simple fact is of
extreme importance when generating BF code programmatically.
The program above is also straightforward – it sets cell 1 to 2, then loops over it and increments cells 2 and 3 by one on each iteration. Once we are out of the loop we have an empty cell No.1 and cells 2 and 3 both containing 2 (the original value of cell 1). Now the important part of keeping the illusion up: the interpreter repositions the data tape to point to cell No.3 an enters a loop in which it increments cell 1 and decrements cell 3. After exiting the loop we see a state where both cell 1 and 2 contain 2, so in effect the program above populated cell 1 and duplicated this value to cell 2.
This was a brief overview of the most basic algorithms for BF which gives a taste of how it operates. Now it is time to add some complexity.
Writing BF programs: dealing with complexity
One problem of BF is that it
becomes really verbose really fast. Consider the duplicator program from above:
[>+>+<<-]>>[<<+>>-]. I have removed the initialization because it could be
used as a form of macro expansion each time one needs to duplicate a cell. This
particular subprogram would work with assumption that data tape is properly
positioned, would copy the current cell over to its right neighbor and
would use a cell one over to the right from the current one as a temporary storage.
Any non-trivial program would need to store some data. This data will be placed
somewhere on the data tape. Some bits of this data may become irrelevant during
run-time or could need an update, potentially from another such piece of data.
A duplicator would work great to achieve this provided that it uses correct
intermediate cells and positions correctly within both loops. This means
that a duplicator must be amended to contain correct number of > and
< commands for proper positioning.
BF has been discovered by mankind about 30 years ago. During this time a lot of algorithms have been developed for this model. To maintain algorithms universal and also to simplify their handling a shorthand notation was introduced and became rather popular. In this notation data cells are given human-readable names like ‘x’, ‘y’ or ‘temp0’. Each appearance of such a symbol in an otherwise correct BF code must be interpreted like: “Now position data tape in such a way that current cell is temp0”. In such notation duplicator becomes significantly more user-friendly: suppose we want to copy ‘source’ cell to ‘destination’ cell via ‘temp’ cell. Then the code would look like this:
[destination+temp+source-]temp[source+temp-]
This simple amendment makes code snippets portable – they do not rely on fixed addresses anymore and could be easily embedded into more complex programs. This is exactly where I said “A-ha!” and started automating this process.
On the surface the task is very straightforward: there is a number of basic algorithms each of which could be independently embedded into a final program, a scheme for naming these algorithms and another one for managing cell names could be devised and that would result in a simple and good enough “compiler” for generating BF code.
This is exactly what I tried to do. The path forward turned out to be rather educational and fun (and it also took quite some time because other things kept distracting me from it). Here I present a (mostly organized) collection of notes accumulated while on it.
A Compiler: the modest beginnings
The first thing which was rather obvious from day 1: the resulting higher-level language will be rather primitive by any standard, something along the lines of PL-I, and will be more like a shorthand for writing BF rather than a proper abstraction tool. (There was yet another side-track where I experimented with implementing a combinators engine on top of BF, but that is again a different story which I’ll maybe tell some other day). Thus a typical program would consist of variable declaration section and some code which would use these variables. I did not feel like adding any inference logic, it somehow felt like an overkill. The standard workflow for such task assumed that I had to come up with a grammar for the language beforehand, then get myself a parser and process a syntax tree. That also felt a bit like too much work, so I spent quite some time postponing specification.
Then one day it struck me – since the translator tool is to be primitive I could probably skip the grammar definition part completely! Suddenly I recalled reading [Theory of Computation for Programmers] where a “compiler” was built around Ruby: valid Ruby constructs were used to generate low-level code, and a program in this new language was both valid Ruby (in the context of definitions) and valid whatever-it-was-called that compiled to target architecture. “I’ll do the same” thought I, “I’ll piggy-back on Python, will create abstractions that are both valid Python and are capable of generating proper BF code or modifying compiler state”. I drafted a couple of sample programs to get the feeling of it:
VAR("X, Y, W", BYTE)
VAR("I", INT)
PROG(
SET(X, 5),
SET(Y, 2),
SET(I, MUL(X, Y)),
WHILE(X, PROG(
DEC(X),
SET(W, ADD(W, Y)),
PRINT("In loop: ", W, "\n"),
))
…and started churning code because I liked how it looked. (I chose upper case to make it look more like some historic Fortran printout and also to make my functions visually distinct from internal helpers and occasionally from Python keywords).
It started out extremely smoothly:
def move_to(x):
return ">"*x
def return_from(x):
return ">"*x
def INC(x):
return move_to(x) + "+" + return_from(x)
def destructive_copy(src, dst):
return (move_to(src) + "[-" + return_from(src) + INC(dst) +
move_to(src) + "]")
def non_destructive_copy(src, dest):
tmp = allocate_temp()
out = (move_to(src) + "[-" + return_from(src) + INC(dst) + INC(tmp) +
return_from(tmp) + "]" + destructive_copy(tmp, src))
Allocation of temporaries was implemented in the most straightforward way
possible: with a counter which would be incremented and returned by
allocate_temp() and decremented by deallocate_temp(). Everything
essentially operated on raw addresses. Most basic primitives were as simple to
implement as the snippet above. Just a couple hours of typing and I had a nice
and operational PoC!
Actually my first couple attempts were not successful: they suffered badly from distractions and mission creep. It also turned out that I tried bringing in too much unnecessary complexity into the project. The code above is taken from the third iteration when I realized that I do not need to support too many types and that I can easily live without polymorphic functions, at least in the beginning. And that I maybe don’t actually need any types except the base one. But that did not occur to me in the beginning so complexity won a couple of rounds. Those early attempts also suffered from other experimental decisions which were introduced too early like fixed scratch space in the beginning of data tape for temporaries (which initially looked like a good idea – temporaries are usually accessed often, so why not put them where they will be close at hand? And have like 16 of those, 16 will be enough for everyone, right? In practice I found that this limit would constantly get breached because any non-trivial program requires LOTS of scratch space), but most importantly they suffered from the fact that program execution order in BF fundamentally differed from the order in which a generative program would be interpreted.
Consider standard BF algorithm for implementing “if (x) then (code1) else (code2)”.
temp0[-] temp1[-]
x[temp0+temp1+x-]temp0[x+temp0-]+
temp1[
code1
temp0- temp1[-]]
temp0[
code2
temp0-]
This code is universal, i.e. any
value of code1 and code2 could be used, including, but not limited to nested if
expressions. Note, that the code relies on two temporary variables, temp0 and
temp1. When a BF interpreter reaches such block it presets temp0 and temp1,
then proceeds with executing either code1 or code2. Both code1 and code2 could
be using some other temporary variables, an arbitrary number of those.
Now consider a hypothetical IF function defined like this:
def IF(condition, code1, code2):
...
In a PL-B program it would be used like this:
...
IF(CONDITION, PROG(...),
PROG(...))
Here lies a problem. Remember, that IF is in its essence a Python function. Which means that
before calling this function its arguments must be evaluated. Which means that
PROGs for both branches will be evaluated before IF. Each of these functions
could request a number of temporary allocations. Then they would proceed with
using these allocations inside the code they wrap and will deallocate them once
the code is generated. This creates a problem for IF: it must allocate two
temporaries, do this before branches do their allocations and maintain these
allocations until after both branches have deallocated their allocations.
Otherwise a very unpleasant clash will occur. Suppose that by the time the
compiler reaches IF in the code above we have N allocated variables. Suppose
that both branches require two temporaries each. This means that when processed
by Python interpreter in standard left-to-right order then branch would
allocate N+1th and N+2th variables, generate code that touches them and
deallocate them. Now else branch would do the same and would rely on the same
cells. After it is done there are still N allocated variables.
When code generation is done for the branches it is time to generate code for IF itself. Which needs two temporaries. And there are N temporaries allocated. Which means that IF is free to use N+1th and N+2th cells. Which are also coincidentally modified by both branches because at the time of branch code generation they were free! Now IF flow becomes completely disrupted because there are absolutely no guarantees that any of the branches would preserve correct state of temporaries. Moreover it would be highly illogical to demand such preservation since the very nature of scratch space is to be used without any fear.
And thus is should become very clear that BF evaluation order differs from Python. This difference in evaluation order had almost convinced me to just specify a parser and never attempt this folly again when it suddenly dawned on me: thunks! I could simply pass wrapped code objects around without evaluating them. Having something like
IF(condition, lambda: PROG(...), lambda: PROG(...))
would enforce necessary order. Now that would look very suspicious in code, so I added a simple translation rule to “preprocessor”, namely to replace any occurrence of ‘THEN:’ and ‘ELSE:’ with ‘lambda:’. It stopped being Python compatible, but nevertheless it remained just two direct substitutions away from it. After some considerations I decided that I can live with it.
This cleared a path for multiple helpful functions such as AND, NOT, ADD and
several others. After some thought I amended my internal contract to return
not just a code string, but possibly a reference to a temporary variable
containing a result of expression evaluation. This greatly simplified
building complex expressions like SET(X, AND(NOT(Y), NOT(W))).
The language started taking shape. Many higher-level functions were still missing, however basic logic and arithmetics worked. It was time to start building on top of that.
The next logical thing was to introduce subprograms. Here lied the big issue with BF – no way of jumping to an address. Thus any subprogram code had to be emulated either with substitution or with some rather complicated dispatch mechanism. I have briefly considered the latter and decided to stop on the former. I also added another substitution: ‘BODY:’ as another syntactic mask for ‘lambda:’ to prevent immediate evaluation of a “procedure”. There was still no mechanism of passing values out of subprograms, so I introduced a rule which demanded the use of global variables for getting subprogram results back. One important issue with this approach was recursion and mutual recursion: subprograms looked a lot like actual functions, but they were absolutely not! Recursion, especially mutual recursion, is a very natural way of describing certain operations. Consider arithmetics on signed numbers. Addition of a negative number to a positive number could be delegated to subtraction, and subtraction of a negative number from a positive one could, in turn, be redirected to addition. This would work perfectly well in a normal language with jumps, but would fall into an infinite expansion loop in case of effectively macro substitutions which I had developed. Fortunately I did not encounter this problem before defining INTs.
Finally I introduced arrays. Array processing logic is quite straightforward and well known. One of popular schemes uses two adjacent cells per array element with one used for storing an actual value and another as a helper which is used to locate a cell by index. An interpreter copies an index value into the first index cell and keeps decrementing it and copying over to the next index cell until it reaches zero. Once it reaches zero it uses current value cell contents for requested operation.
Arrays posed a problem since they required adding a separate ARRGET and ARRSET functions to provide access to array elements. I had briefly considered expanding SET for that, but dropped this idea in order to keep SET code reasonably simple.
This concluded the first phase of building the most basic compiler. Now it was time to add actual functions to it.
On integers and reals
Remember my definition of a useful computer: something that computes sines fast enough. To compute a sine one would need a way of representing real numbers, and preferably also a way of representing integers.
By the time I got there it was already obvious that BF as computational model is not exceptionally fast, and some operations could take significant amount of time when operands are sufficiently big. For example, GT and EQ both are affected by this with processing time growing linearly with compared values from hundreds to tens of thousands of steps.
My initial plan was to use compact multy-cell representation for integers. On the surface it was a decent idea – just four adjacent cells would hold numbers of up to 2^32. However my experience with GT warned me against that: any operation on such number would require multiple computations of GT with large operands, so it was absolutely not an option. Since GT performs better on smaller values it became obvious that using a representation of numbers that relies on smaller values of individual digits would eventually work better.
An alternative which I initially did not appreciate much was to introduce some long math on arrays. An array of ten elements could represent numbers from -999999999 to 999999999 (and two flavors of 0 as a bonus) with one element devoted to representing sign and remaining nine to representing digits from 0 to 9. It turned out, that for basic math it was sufficiently fast staying in the range of a few tens of thousands of steps per operation no matter the actual value. The overhead price was paid every time, but it turned out to be relatively small compared to my estimates for more compact format. The downside was the waste of large swaths of memory, but I deemed this trade-off worthy. The problem of negative zero was resolved by making sure that all primitives which could have resulted in a negative zero were thoroughly covered with tests and no primitive operation resulted in a negative zero. All higher-level operations would exclusively use lower-level and tested operations and no negative zero would ever appear.
The language started to become even more appealing, now it became possible to compute Fibonacci numbers in a relatively small number of steps:
* Welcome to Fibonacci computer!
* It computes n-th Fibonacci number.
* Please enter n>2: 40
===
* Result is: 102334155
The snippet above contains output stream of a program that computes moderately large Fibonacci numbers. The computation above took 14778927 steps which translates to about fifteen seconds on slower interpreters (like the hardware ones I have described in my other posts). This is significantly faster than a couple minutes which I need to compute the value using pen and paper. It is obvious that the model does help with at least some computations after all!
Introduction of integers created another problem: now my functions had to become polymorphic and learn about type coercion. When performing SET(X, val) I would need to check if val was an integer or a byte and act accordingly. When doing ADD(X, Y) I would need to make sure that both X and Y are of the largest fitting type. All of a sudden this introduced some significant complexity to my code. And given that all these decisions and dispatch had to be made on the fly, without the benefit of an explicit data structure for storing necessary context all existing functions risked becoming overcomplicated.
I chose a different way of dealing with this. Being inspired by languages of yore I offloaded all this complexity on my users: by introducing a separate set of functions for working with integers and mandating explicit conversions I kept my codebase complexity at bay while simultaneously complicating lives of my potential users (likely just mine). Given that any non-trivial program that could suffer from such poor design choices would not be computed by any BF interpreter before the thermal death of the Universe I was pretty sure that no one would suffer too much. And this is how I ended up with a family of INTADD, INTSUB, INTSET etc., functions. On a separate note INTPRINT ended up being significantly faster than regular PRINT for numbers between 200 and 255.
While addition and subtraction of integers was rather straightforward INTMUL and INTDIV proved to be trickier. First of all, nice and fast algorithms like Karatsuba’s multiplication did not map on BF model that well. Second, I ended up introducing restrictions on both division and multiplication to save execution time.
Consider multiplication of two integers with N and M digits. Multiplication result will have N+M digits. Thus to be able to honestly multiply two nine digit INTs I would need to allocate a temporary storage of 18 digits and properly trim the result once it is known. This is not difficult to achieve programmatically, but would have been prohibitively expensive computationally when run by a BF interpreter. I had to introduce and arbitrary rule for multiplication which required operands to contain less than nine digits in total. This allowed me to safely work with any number less than or equal to 10000 which I deemed enough for experiments and demos. And since all limits were derived from a constant determining the number of digits in an INT it would have been trivial to increase the limit once I was confident that it won’t sink performance. Integer division was not that problematic, it was just sluggish and required a couple of rounds of optimization later on.
Finally I had everything I needed to implement reals. There are many good ways of implementing them, so I chose the one that I already had at my hands: fixed point representation with one decimal digit before dot and eight after. This was enough for computing sines and that was all I cared about at the moment. I never considered floating point worth it for a BF compiler and fixed point is usually one or two constant changes away from accommodating any necessary precision. With, say, INTs being 48 digits long I could have easily had fixed points capable of representing numbers from 10^-24 to 10^24 which is more than enough for any practical computation. Now the question was how many aeons would pass before a BF interpreter finishes setting up just a single such number. I did not have an answer at that moment and decided to postpone answering this question until I had more data.
To distinguish reals from integers I decided to introduce a family of FXPxxx functions. Actually I had almost everything I needed except for FXPMUL , FXPDIV and FXPPRINT: all other operations were effectively aliases to operations on INTs. Both multiplication and division proved challenging. Now I had integers no more, so I had to take care of rounding errors. I spent some time sketching various approaches to correct handling of rounding errors and proper rounding, but ultimately I decided to do nothing about it. Correct rounding was computationally expensive and required extended storage – something I tried to avoid, especially adding more run-time computations. Thus I decided to give it a try and see how badly I will miss my sines with just dropping all digits that won’t fit into nine bytes.
Multiplication was somewhat straightforward, the only thing I had to do was to shift second multiplicand to the right until only three digits remained. This was a very dangerous decision since it introduced dependency between total error and multiplication order, moreover, it could produce different error magnitudes for different input values. Unfortunately this was the price I had to pay for simple (in BF word that means significantly faster) algorithms. Once again I decided to give it a try and hurled more robust algorithms to the pile of tech debt.
The relevant part of multiplication of two FXP variables var1 and var2 is presented below
PROG(
INTSET(var1_t, var1),
INTSET(var2_t, var2),
SET(var1_rshift, 2),
SET(var2_rshift, 5),
WHILE(var1_rshift, PROG(
_int_shift_right_in_place(var1_t), DEC(var1_rshift))),
WHILE(var2_rshift, PROG(
_int_shift_right_in_place(var2_t), DEC(var2_rshift))),
INTMUL(var1_t, var2_t, res),
_int_shift_right_in_place(res),
).code
The code is no more than shaping of variables to prepare them to be multiplied as integers:
PROG(
_clear_int(interm_res),
_clear_int(res),
SET(signs_differ, _xor_two_bytes(INTPOSITIVE(var1), INTPOSITIVE(var2))),
SET(ppos, SUB(_int_num_of_digits(var2), INTARRAYLEN)),
SET(var2_diglen, _int_num_of_digits(var2)),
WHILE(var2_diglen, PROG(
SET(tmp, ARRGET(var2, ppos)),
WHILE(tmp, PROG(
_int_add_both_positive(res, var1, interm_res),
INTSET(res, interm_res),
DEC(tmp),
)),
INC(ppos),
DEC(var2_diglen),
IF(var2_diglen, lambda: _int_shift_left_in_place(res), lambda: NOP()),
)),
IF(signs_differ, lambda: INTNEGSELF(res), lambda: NOP()),
)
The code for integer multiplication is essentially a replication of elementary school manual multiplication algorithm. Note that this code is a mixture of PL-B and Python – this turned out to be a productive method of building the compiler.
Another option that I did not investigate hard enough (and which might end up being a significant boost to multiplication) is prepopulating data tape with a multiplication table. I hypothesized that this could ultimately translate multiplication into a sequence of searches, but had never got to properly testing this out for practical reasons: I needed way more flexible arrays for that, a bit more flexible interppeter and a more flexible testing framework. It would also have required an extensive search for optimal table size vs. primitive operations penalty and might have even required to place the table after all areas that were expected to be used during run time. However this would have required analyzing the code which my overly simplistic tools was ill suited for. As a result I have mothballed this subproject as well.
I wish I could have done the same trick with division, but unfortunately it required more checks to ensure correct value is used on each step. I also had to carefully multiply both the remainder and the result by ten when a remainder would end up smaller than divisor. I got this algorithm as a result:
PROG(
_clear_int(remainder_t), _clear_int(int_tmp),
INTSET(remainder_t, var1),
INTSET(divisor_t, var2),
SET(outer_loop, 1),
PROG(*[INC(outer_condition) for _ in range(INTDIGITSNUM)]),
WHILE(outer_condition, PROG(
SET(inner_loop, _int_gtoreq_both_positive(remainder_t, divisor_t)),
IF(inner_loop,
# THEN can divide now.
lambda: PROG(
_clear(count),
WHILE(inner_loop, PROG(
INC(count),
_int_sub_both_positive(divisor_t, remainder_t, int_tmp),
INTSET(remainder_t, int_tmp),
SET(tmp, OR(_int_gt_both_positive(remainder_t, divisor_t),
_inteq_both_positive(remainder_t, divisor_t))),
IF(tmp,
# THEN we can continue
lambda: NOP(),
#ELSE break the inner loop
lambda: _clear(inner_loop),
),
),
),
ARRSET(res, outer_loop, count),
_int_shift_left_in_place(remainder_t),
),
# ELSE have to shift remainder and result
lambda: PROG(
SET(fd, ARRGET(remainder_t, 1)),
IF(fd,
# THEN (not zero)
lambda: PROG(_int_shift_right_in_place(divisor_t),),
# ELSE
lambda: PROG(_int_shift_left_in_place(remainder_t),),),
ARRSET(res, outer_loop, 0),
)),
INC(outer_loop),
DEC(outer_condition),
)),
)
Once again an almost-verbatim translation of an elementary division algorithm.
Note that I have to use lambda: in places where I would have used THEN: and
ELSE: in a regular program – there is no preprocessing step for the compiler
itself. Also note the abundance of internal (marked with _ prefix) functions:
these are more specific versions of operations which result in shorter code.
For further details on why this was important see the section on optimization.
The code above also does not handle signed division. The change to add it is
trivial, but I was in a hurry to get my hands on an ultimate test program
and just threw sign handling division to the tech debt pile.
Because nothing stopped me anymore from writing the ultimate test program and finally learning how bad BF platform actually was!
On the ultimate test program
For quite some time I have been holding a belief that a useful computer should be able to compute a value of sine of an angle at least faster than me. Thus I used this minimal usability rule to determine if something is computationally useful. BF compiler was not an exception: I decided to consider it more or less completed once it was capable of compiling a program for computing a sine of an angle.
In most cases first three elements of the series for sines produce good enough results:
(-1)ⁿx²ⁿ⁺¹ | ∞
sin(x) = Σ ---------- |
(2n + 1)! | n=0
So I implemented the program to compute sines in the most straightforward way. One of the intermediate variants is presented below. It lacks most of user facing parts and expects angles in radians. Conversion from degrees and user prompts could be trivially added to it.
VAR("X0, X1, X2, X3, T, I, D, RES", FXP)
PROG(
FXPSET(X0, 0.785398), # Input value
PRINT(" * computing for x = "), FXPPRINT(X0), PRINT("\n"),
FXPMUL(X0, X0, I), FXPMUL(I, X0, T), FXPSET(X1, T), # X^3
FXPMUL(X1, X0, X2), FXPMUL(X2, X0, T), FXPSET(X2, T), FXPSET(T, 0), # X^5
FXPMUL(X2, X0, X3), FXPMUL(X3, X0, T), FXPSET(X3, T), FXPSET(T, 0), # X^7
FXPSET(D, 6.0), # Second term: computing and using it.
FXPDIV(X1, D, I),
FXPSUB(I, X0, RES),
FXPSET(T, 0), FXPSET(I, 0), # Third term: computing and using it.
FXPSET(D, 1.2), FXPDIVBY10(X2), FXPDIVBY10(X2),
FXPDIV(X2, D, I),
FXPADD(RES, I, T),
FXPSET(RES, T),
FXPSET(T, 0), FXPSET(I, 0), # Fourth term: computing and using it.
FXPSET(D, 5.04), FXPDIVBY10(X3), FXPDIVBY10(X3), FXPDIVBY10(X3),
FXPDIV(X3, D, I),
FXPSUB(I, RES, T),
FXPSET(RES, T),
PRINT(" * Answer: sin(x) = "), FXPPRINT(RES), PRINT("\n"),
The code uses a number of temporary variables to precompute and store temporary data. The amount of temporary variables is balanced to make it both moderately fast and easier to follow. It is possible to reduce the amount of variables further, but it does not significantly affect the overall speed. Going to 5 variables vs 8 results in 2.6% number of steps reduction which is not fundamentally worth it. In the rest of the text I will use sine code listed above as the benchmark for all PL-B processing.
On testing and debugging
From the very first attempt it was clear that the tool has to be extensively tested. The only question was – how exactly. Standard unit testing was only partially applicable, so I had to come up with a way of testing the entire compiler that would point me to at least a subsystem that caused an issue. I also believed that I would need some mechanisms to interactively debug generated code. As a result I split my efforts into two arcs, one for building an instrumented interpreter and another one for defining a testing framework for automatic verification of as many compiler aspects as possible.
Initially I believed that properly instrumented interpreter would be crucial for success. That is why I iterated through a number of progressively more sophisticated interpreters. I thought that I needed something similar to gdb or pdb, but for BF, thus I wrote several generations of more and more intricate BF interpreters which allowed me to nicely observe pointers movements (I cursed a lot while making it look pretty with ncurses), make arbitrary number of steps in any direction, i.e. allowing stepping forward and back in time (moving back in time required keeping a list of pairs for each modifiable entity where head represented a moment in time in tics and tail represented a change), breakpoints and other helpful amenities. I learned really fast that all these tools were not very helpful when debugging machine-generated BF. The problem was as usual in the nature of BF: the low-level code always turned out to be exceptionally long and repetitive, and manual tracing stopped being an option very fast. Even programs with rather primitive semantics would end up being thousands of symbols long, jumping through them was absolutely not fun and local BF context usually made no sense. I tried working around this program by making the compiler generate context data for each compiled piece. A second file would be generated in parallel to BF code. This debug file would contain as many lines as there were symbols in a compiled BF piece. Each line would contain all context the compiler had at the moment of compilation: the entire call stack and memory allocations (every temporary cell would get distinct name consisting of function name that requested it, temporary variable name and an ever-increasing number as a distinguishing suffix: “SET::tmp::2045” so it would be easy to see at a glance what this cell was currently used for). Then an interpreter would use this debug file to augment its output when stepping through code or when encountering a breakpoint. Moreover, such instrumentation allowed me to be more precise about breakpoints: before it I was effectively limited to breaking on user-defined variables modifications because temporary cells were regularly re-assigned and re-used. With this change I gained the ability to specify in which context I would like to observe the interpreter’s behavior in greater detail.
Compiler instrumentation part was as smooth as it could be: one context-providing decorator was enough to produce all data I would ever need. On the downside it slowed compilation to a crawl (and it was not too fast to begin with, more on this in compilation optimization section). Building yet another BF interpreter that would make good use of this data proved to be a much bigger challenge since I had to think a lot and experiment with usability of the resulting tool. I started making an interpreter with a ed-inspired interface (or one might say gdb, but I preferred to think of it as of a weird offspring of ed). I added a number of commands to start/stop execution and to add breakpoints and then got stuck with getting a clear reconstruction of compiler’s path through the code.
At some point I tried generating a full trace of a program execution and then using a smart replay tool to observe changes to memory cells that I deemed important. This was a bit easier to implement, however the resulting traces were huge, spanning tens of megabytes for rather trivial programs. It felt like a dead-end.
Eventually I gave up on this effort: at some point I realized that 95% of the most exquisite-looking bugs are, in fact, caused by not properly cleaning temporaries. Once I introduced proper automation for temporaries allocations and cleanup I saw a drastic reduction in the number of failing tests and strange behaviors. Interestingly enough one of a lesser, temporary helper tools from my testing rig proved to be invaluable for detecting these sorts of failures, more on it below.
The remainder of issues turned out to be rather straightforward too: mostly logical errors in higher-level functions (remember, that most of the compiler is written in the same language it compiles). It appeared that catching them with memory validator and a rare debug PRINT in the code was much faster and easier than slogging through generated code with a debugger one step at a time.
While manual testing and debugging made some sense during early implementation phase and very occasionally later it was clear from the beginning that some sort of testing automation must be present. It was also clear that the compiler must be tested as a whole, i.e. it must compile some sample programs, then these programs must run and the state of the interpreter after running these programs must be validated against expectations. The state I was interested in was memory contents, stdout contents and a pointer to the last consumed element of stdin.
In the earlier attempts I tried using Python’s unittest module to structure the tests, but it was not very handy: the tests turned out to be too verbose and either disconnected from test code snippets (if I chose to store code in separate file), or even more verbose and rather clunky if I chose to store the tests snippets as strings right next to the tests themselves.
At some point I realized that I could benefit from an intermediate test-definition language which I would embed into code snippets. This language did not need extravagant expressiveness since all I wanted to verify was effectively just stdin and stdout states and also occasionally memory state. The language also had to be terse and not obscure the snippets. My goal was to have most test snippets and test definitions fit on a standard screen. Thus the language had to use horizontal space well.
I decided to use S-expression-looking syntax for the task since I had a reader at hand and found it a little more aesthetically pleasing than json. I settled for a test description format where the head of such expression contains a long human-readable test description and a tail consists of pre- and post-conditions for the tests: stdin contents, expected stdout state and optionally expected memory state. To make sure descriptions won’t interfere with compilation they were put on commented out lines. To distinguish them from any other comments I added a beak right after pound symbol. An example of a test could be found below:
#> (if-works-in-general
#> (out "!")
#> (mem X 0...)
#> )
VAR("X")
PROG(
SET(X, 5),
IF(X, THEN: PRINT("!"), ELSE: PRINT("*")),
)
Here I used a yes or no phrase to name the test (I chose to have yes/no displayed along a test description during a test run), then added a constraint on stdout: I expect to see a single exclamation mark in it, then added another constraint on memory: I said that I did not care about contents of the first element of data tape and denoted that with X, and stated that any other cell after the first one must be empty (0… denotes exactly that). An exclamation mark was chosen as the smallest visually meaningful ASCII character. The initial idea was to make code as compact and short as possible and thus to use symbols which require as few additions to generate them as possible. This proved to be futile due to the fact that other operations clearly dominate rare output generation, this is reflected by a later transition to * as negative result symbol.
The mem clause was initially considered as a lesser helper which in practice turned
out to be invaluable. My original reasoning was that having constraints on memory would
make tests too brittle: I might decide to add more test cases which would modify a
variable or two, or I might switch to a different allocator which would shuffle
variables in a yet unpredictable manner. I did not want to invest into semantics
extractor for the tests (remember – I was still trying to stay within the confines of
not properly parsing the code and keeping things “simple”), so originally was not
planning on using this clause at all. Here I must belatedly confess that I lifted the
entire concept from BF interpreters verifier: since I had a habit of periodically
rewriting BF interpreters to either make them instrumented or to test some concepts I
needed a universal set of tests for such interpreters. I used the same format to write
a lot of one-liners of the following shape:
(empty-cell-leads-to-skip-of-bracketed-code (code [+]) (mem 0...) (steps< 10))
So I had a lot of ready to reuse parts, and mem was simply there, waiting to be
put to some use. It turned out that having a constraint on memory cell being empty
beyond variables allocations proved extremely useful for catching forgotten cleanup
bugs. This did introduce some coupling between test definition and code snippets,
but for most tests the distance between coupled parts was about five lines, thus
I deemed it acceptable. (It was way worse than that for arrays, but I grew distracted
by other things and kept coupling in place).
A typical verbose test run looks like this:
Expected stdout: !
Captured stdout: !
if-works-in-general yes
=
Compilation : 0:00:00.002740
Execution : 0:00:00.011263
Total : 0:00:00.187606
Line count : 4
Code length: 154; steps taken: 402
Execution speed: 35.7 Kstep/s
A quiet run does not contain expectations and observation unless they mismatch. During a test run I measured compilation and execution times as well as other statistics about the code and interpreter. This data proved invaluable for compiler optimization.
On optimizing the compiler
Now the code could be generated and every new generating function would be immediately covered by quite a few test cases. It started to become progressively harder to mess with basic functionality, to the point where I stopped running the entire test suit on each change: the base became rock-solid, and it also started taking too long to run the full suit.
The first few dozens of tests were awesome and blindingly fast: a couple of seconds
of cheerful foo-works-when-bar-and-baz yess scrolling through my screen and
the testing was done. But the more tests I added and the more complex functions I
started to compile the longer it took for tests to complete. Running all suit for
15 seconds was a little disruptive. Running it for a couple of minutes was enough
to let my mind wander a bit too far. I had to do something about it. My initial
reaction was to consider it to be the price of doing busyness with BF – a lot of
back-and-forth, no assignment per se etc. I switched to running just the subset
of tests for a feature I was currently working on, occasionally for a feature with
a freshly discovered bug and the entire suit was left for a pre-commit check.
The problem was it was still not enough! And surprisingly enough it turned out
that compiler started to spend way too much time generating code. Thus I ran out of
excuses for postponing optimization and dedicated some time to figuring out how
come simple substitutions started taking significantly longer than repeated shufflings
of a single bit across a long data tape.
My initial suspect was the automation I used to generate debugger-friendly variable names. Remember “SET::tmp::2045”? Such name had to be either hardcoded or generated. In the early PoC stage it was hardcoded indeed: every function used to begin with an ugly preamble:
def FOO(var1, var2):
tmp = _allocate_temp("FOO::tmp")
...
Such boilerplate sections were distracting and hard to maintain properly: boilerplate
makes it super easy to copy it around. Once copied it has to be modified, but since it
is a boring chore it is extremely easy to forget to do so. Here I had to make sure that
both function name and variable name are correct. In other words I had to repeat
myself. I did not like it and initially I added a simple helper that would use
inspect to get caller frame, would extract caller name and code context from it,
parse the leftmost part of assignment and allocate and return enough variables.
Now boilerplate like
tmp = _allocate_temp("FOO::tmp")
foo = _allocate_temp("FOO::foo")
bar = _allocate_temp("FOO::bar")
was boiled down to
tmp, foo, bar = locvars = _allocate_temps()
Much tidier than before! I also decided to keep a separate reference to the entire tuple of temporary allocations to make sure they are correctly prepared for usage and later disposed of:
tmp, foo, bar = locvars = _allocate_temps()
code += _clear(*locvars).code
... # produce some code that uses these allocations.
code += _clear(*locvars).code
_deallocate_temp(*locvars)
return (code, retval)
Still quite a lot of boilerplate, but much better than before and harder to introduce
a sneaky bug. (With such addition I tended to forget to add the final cleanup code
completely which could be easily detected with mem clause and trivial to fix).
Intermezzo: automatic boilerplate application
I do not like boilerplate. It is far too easy for me to forget adding it, or to forget adding enough of it. This often results in fun bugs. The biggest source of boilerplate as I have mentioned above was code to initialize and recycle temporary, PL-B instruction scoped variables. Since every non-trivial high-level function required at least a couple of those, every such function would start with an allocation and end with cleanup:
tmp1, tmp2, tmp3 = locvars = _allocate_temps2()
# code that uses locvars
out += clean(*locvars)
_deallocate_temp(*locvars)
Forgetting to clean up would sometimes result in a very odd-looking issues and I have spent a couple of
very frustrating evenings furiously scratching my head while trying to figure out why
a perfectly fine algorithm or a trivial modification to a test would produce wrong results. Once it dawned on me that
forgetting a clean(*locvars) could produce all sort of surprises I reduced time spent on debugging
weird issues by more than 90%. It also became very obvious that this is a very good candidate for
automation. Moreover, I did not like the looks of code with these explicit allocations: they attracted too much
attention to themselves. It would have been awesome if I found a way to just list all the names I needed,
got these names introduced into the local scope and then had them recycled once an instruction
finished code generation.
My first hunch was to do that with some clever context managers. They seemed to be perfectly suited for this:
on entering a context I could allocate a new temporary variable and then deallocate it on exit. But
this would leave the hardest part – cleaning, – on me. (While deallocation is important it is not
as critical as cleaning temporaries: the worst thing that could happen is a memory leak and critical
loss of performance). Further, I could not come up with a non-ugly way of writing the with statement.
No matter how I tried I would always end up with a gross chain of _allocate_temp() calls.
At some point I declared context managers the winners and turned to my second most favorite tool: to decorators. The idea was pretty good, at least on the surface: having something like
@uses_temporary_vars("tmp1, tmp2, tmp3")
inject these variables dynamically into surrounding scope of a decorated function and then to just use these variables within the decorated function as if they were always present outside. Easy! Actually not so much: it won’t work this way. After some experimentation it turned out that it is hard to beat scoping rules and make Python behave as if it was dynamically scoping. While it was technically possible to squeeze the variables through global namespace or by defining a dictionary in a wrapper (prosthetic environment?) and accessing temporary variables implicitly through that dictionary both results proved to be exceptionally ugly when implemented.
Since I did not have to run this in prod I decided that I could afford playing dirty. Risking to jeopardise my entire mission I made a decision to summon the power of ast module. This was one of the great taboos from the early days of PL-B. Touching ASTs was considered a capitulation to parsers – just walking a tree would have immediately resolved most of the problems I spent hours carefully working around. Not fun at all. I could have written a parser on day 1, too easy. But eventually I realized that I needed ast to amend the compiler itself and not the code it compiles, became relieved and proceeded with the change.
The idea was pretty straightforward. Since I could not cleanly mess with enclosing environments I could mess with the code. All boilerplate parts followed the same pattern in the code:
boilerplate_premable
actual_code
bolierplate_postamble
So if I had a text of a function then adding boilerplate to it would have equaled to prepending some text
to it and then appending some more text. If I had a macro processor siting somewhere between my code
and the interpreter that would have been trivial (remind me to tell you the story about the time when I tried
funneling python code through m4 before feeding it to an actual interpreter). Unfortunately I did not have
that, but I could always read function code with inspect. Moreover, the read code could be parsed with
ast.parse and then compiled to bytecode with built-in compile. The only thing left would be to
carefully swap the original compiled code of the old function with the freshly compiled one.
I ended up with the following implementation:
def uses_temporary_vars(vars_to_inject):
def wrapper(f):
old_code_obj = f.__code__
preamble = [
f" {vars_to_inject} = locvars = _allocate_temps2()",
" out += _clear(*locvars).code"
]
cleanup_range = "[1:]" if "retval" in vars_to_inject else ""
cleanup_code = [
f" out += _clear(*locvars{cleanup_range}).code",
f" _deallocate_temp(*locvars{cleanup_range})"
]
f_code = inspect.getsource(f).splitlines()[1:]
new_code = f_code[:2] + preamble + f_code[2:-1] + cleanup_code + [f_code[-1]]
new_code_parsed = ast.parse("\n".join(new_code))
new_code_compiled = compile(new_code_parsed, old_code_obj.co_filename, "exec")
f = FunctionType(new_code_compiled.co_consts[0], f.__globals__)
@wraps(f)
def inner(*a, **k):
return f(*a, **k)
return inner
return wrapper
Note the f = FunctionType(new_code_compiled.co_consts[0], f.__globals__) part which swaps the original
code with its improved version.
This decorator turned out even better than I originally expected. Unfortunately it did not work either. Turned out, that I have already tried cheating around the need to manually specify all arguments to allocator. However back then I did not anticipate that the calling code could be ephemeral and won’t exist on the file system. I could have amended the basic allocator once again, but I decided to just manually stuff enough low-level allocator calls to make it work. After that it worked like a charm.
Well, not like a good charm to be honest, more like a bargain mediocre second-hand charm
from a charms thrift store. While cobbling the implementation together I chose to ignore the fact
that there could be more than one line of text in the beginning of the function (I injected by
physical lines count i.e. it did not matter if the first line was code, a docstring or a comment
– a preamble would appear right after it), I did not account for multiline argument to the decorator (
that would also confuse the offsets) and totally forgot about properly passing arguments
with default values to the freshly compiled function (moreover I hardcoded code object position
within co_consts tuple which would fail miserably when there are default arguments).
However despite all these shortcomings the decorator worked surprisingly well.
Now back to run-time optimizations.
Run time optimizations (continued)
inspect is a handy module that provides an easy to use window into interpreter’s
internals. Unfortunately inspection of stack in runtime is somewhat expensive.
A lot of code is written in Python and the interpreter takes quite some time
to construct all auxiliary objects. It is not a big deal when a program inspects the
stack occasionally, but starts to become a problem when it is done regularly.
The first and easy win was to hardcode a name of just one internal function which was used extensively – a helper that would generate a constant to be used in an expression. It would take a high-level constant, then allocate a fresh temporary cell and then generate code to increment this new cell to the requested value. It turned out, that this would happen very often. This, in turn, would cause lots of unnecessary stack examinations. Thus I decided to hardcode one single name. This alone shaved off about 10% of compilation time.
Now a quick glance at profiler data told me, that even after hardcoding a name
for the worst offender resulted in thousands of calls to inspect for a moderately
complex program. This looked very expensive. And since this was Python I decided that
it is time to write my own C version of inspect. I dug into the interpreter’s code
and quickly realized that under the hood inspect relies on sys._getframe() call
and then shapes and enhances Frame object which it receives. “Alright”, I thought,
“I’ll check sys._getframe() implementation, rip everything that I don’t need and
will speed everything up 100x”. It turned out, that there is almost nothing to rip
out of _getframe(), it is really minimalistic, and apart from constructing a couple
of objects it mostly follows several pointers and returns one to the caller. It was
very unlikely that I could beat that. Ok then, there was still this context-generating
part. On the plus side a Frame object from _getframe() contained almost all the data I
needed, on the minus side the only way to access current line was to extract it from
a file with code. Thankfully the compiler was built around multiple repetitions of
just a few dozens of functions, so once I saw them all I would not need to check them again.
And thus I took Frames supplied by _getframe(), extracted caller name directly from
them, then used another field of Frame to get line number for the caller and used
this data to populate a cache of parsed variable names. Now on each call all I had to
do was to supply a fresh set of variables with properly generated names.
This sped everything up by another 15%. So far so good! This is how the allocator ended
up looking:
class SmartAllocator:
def __init__(self):
self.cache = {}
def __call__(self):
frame = sys._getframe(1)
funcname = frame.f_code.co_name
fname = frame.f_code.co_filename
cache_entry = funcname + "::" + fname
if cache_entry in self.cache:
_vars = self.cache[cache_entry]
else:
lineno = frame.f_lineno
with open(fname, "r") as f:
lines = f.readlines()
line = lines[lineno - 1] # Line numbers start with 1!
_vars = [x.lstrip().rstrip() for x in line.split("=")[0].split(",")]
self.cache[cache_entry] = _vars
ret = [_allocate_temp(funcname + "::" + var) for var in _vars]
return ret[0] if len(ret) == 1 else ret
where \_allocate_temp is a trivial helper that returns an address of a new
temporary variable and which essentially remained intact since the early days
of the “compiler”.
Now I was preparing for a long and enlightening session with the profiler. And I was not wrong, at least not about enlightening part. I have quickly realized that most of the time (about 85% of what remained) was spent on built-in string operations.
1489738 function calls (1475814 primitive calls) in 6.914 seconds
Ordered by: cumulative time
List reduced from 193 to 15 due to restriction <0.08>
ncalls tottime percall cumtime percall filename:lineno(function)
2/1 0.001 0.000 6.915 6.915 {built-in method builtins.exec}
1 0.000 0.000 6.915 6.915 comp.py:2073(compfile)
1 0.000 0.000 6.214 6.214 <string>:1(<module>)
123035 5.745 0.000 5.745 0.000 {method 'replace' of 'str' objects}
3997 0.047 0.000 5.691 0.001 comp.py:30(wrapper)
11365/16 0.008 0.000 5.452 0.341 comp.py:68(wrapper)
5 0.000 0.000 3.976 0.795 comp.py:1969(FXPPRINT)
1140/60 0.007 0.000 2.785 0.046 comp.py:553(PRINT)
1921/428 0.031 0.000 2.456 0.006 comp.py:636(IF)
That was not what I was looking for: I never actually used str.replace anywhere in the code. Except, probably, just one place – in the BF optimizer. Then the realization struck me: I have horribly misplaced the optimizer! This requires some explanation.
Consider a typical scenario: multiple user-defined variables in PL-B program, even more temporary
variables and a very unforgiving interpreter that would generate very unusually
looking results if someone accidentally points it to a wrong location on a data
tape. Thus the easiest way to make sure that we are working on a correct cell is
to always move to that cell via a known location, for example via the first cell.
We always start interpretation from the first cell, so if we want to access
nth cell and modify it then fine – move right n times, do the modification, then move
left n times. If, however we want to modify two or more cells together then after
each modification we better move back to the first cell. In other words, when, for
instance, we are copying from n to m via t we would move to n, decrement, return from n
to the first, move to m, increment, return from m to the first, move to t,
increment, then return from t. This plan is rock-solid and allows one to easily keep
track of where on data tape they are, but it has a flaw – it produces extreme number
of additional tape movements. Suppose that in the example above n, m and t are located
right next to each other with n occupying 100th cell, m, 101th cell and t 102th.
While the copying could be done with several short moves of data tape, direct implementation
of the approach described above would result in 900 extra moves per every single
bit redistribution! That’s a lot and will slow the interpreter down. Fortunately
it is easy to fix. Observe, that moving from nth to first generates n < symbols and
moving from first to mth generates m > symbols immediately after last <. Thus
there will be a <> pair somewhere in the code. Such pair represents a net zero distance
move and could be safely dropped from the code without changing what it does. Repeat
it enough times and you’ll clear your code of any net-zero tape moves. This could
be done in a very straightforward way:
while code.find("<>") > -1:
code = code.replace("<>", "")
Stupid, but very effective in early stages when there is barely enough code to compile
the simplest programs. (Obviously <>’s twin >< must also be dropped).
It took me no time to add such code compressor at some point, it also took no time
to introduce a @compress decorator which would attempt to apply the compressor
to any code generated by any decorated function. Some time around this moment I also
decorated PROG with it. And PROG is used a lot. In fact this is probably the most
used internal function: it is a dirt cheap way to combine logically related
statements together. Or, it was dirt cheap before I decorated it. When decorated it would
dutifully search every tiniest piece of code for compressible patterns,and would
do it hundreds of time for a decently-sized program, even when it does not make any
sense to do it anymore.
Undecorating PROG and making optimization a separate phase yielded an additional ~85% reduction of compile time for most of the programs. Now this was something to talk about. Or not, because the initial problem was completely self-induced. In the early phase of development I still tried to look into code generated by different functions and compressing it before taking a look made perfect sense. The problem was in keeping it around long after it stopped making any sense.
The compression algorithm itself looked like it could be optimized. My initial thought was
“Ok, I am one Knuth-Morris-Pratt implementation away from a blindingly fast
compression algorithm”. It turned out to be a wrong assumption. Before diving into fancy optimizations
I spent ten minutes playing around with replace patterns: it was not unusual to have
long trains of < s followed by similarly long trains of > s, so I figured that it
won’t hurt to try and see what would happen if I added a step for replacing say, ten or
even fifteen <s followed by the same number of >s. This worked really well: having
several such patterns one after another with shorter patterns after the longer ones
added another 3x speedup. Now my test code would be compiled in just 450ms of which
compression would take about 300ms vs 8.5s in the beginning of the optimization.
I did not perform a proper search for optimal sequence of searches and cuts since I
was planning to gain even more speedup with a better algorithm. But no matter
what structure I was about to use just building it from existing code string was
taking about the same time it would take to just run code.replace(…) enough times.
I had to use a better structure from the beginning in order not to loose time on
constructing something more suitable for fast cleanup. Preserving enough of
code’s interface was not a problem, making it fast enough to beat dumb implementation was.
After some additional consideration I decided to remain content with the current
version: it was still absolutely not elegant, but did the job and going from 450ms
to even a 100ms was not worth spending another evening on proper implementation, at least not
now.
Now when the compilation part of tests was fast enough it was time to address interpreter speed.
Below are the stats of compilation of sine provided solely as an illustration:
Compilation : 0:00:00.462004
Of it optimization took:
Optimization : 0:00:00.345891
Code len: 608208
On optimizing the interpreter
My interpreter ended up being very slow. Remember the part about instrumentation? It turned out, that instrumentation hooks and extra counters were as easily forgotten as they were easy to add to high-level code. Each hook and every indirection consumed miniscule additional time per operation, however these amounts added up to very long execution times because of the millions of individual operations performed for even rather trivial programs. I lost my patience rather late in the cycle – I was already writing code to compute sines of angles when the interpreter ground to effective halt. A single iteration would take minutes which was way too long for any meaningful debugging.
This time around I decided to go straight to the root of the problem and to get rid of all overhead in one fell swoop: I have reimplemented the interpreter in C and created a Python module from it. This was very straightforward and took me longer to recall how to structure a C extension than to implement the logic with the entire activity taking a couple hours including testing and fixing stupid mistakes.
It worked even better than I expected. My test code which would run for ~35s on standard interpreter ran for 200ms on the new one. I have immediately put it to use and have observed my test suit to run for less than 15s (versus several minutes before the changes). I was extremely satisfied with the result and made another mental note about the benefits of C extensions: turns out I never used them since my number crunching days and have nearly forgotten about how game-changing they could be.
On optimizing generated code
Now I was ready to get back to sine computation again. It was running really well now: compilation would take about 500ms, execution would take about 1.3s. It was not a problem to debug the code itself and occasionally the underlying functions. It looked great:
* This program computes sines
* of angles in radians.
*
* computing for x = 0.78539800
* ------
* Answer: sin(x) = 0.70709995
Like a real program! To get to this point I had to optimize it a little: I reduced the number of variables to a comfortable minimum (could have reduced it more at the price of readability). The final program would require about 154M steps to compute a single sine. This felt like a lot, so I delved into the compiler to make it generate more efficient code.
It turened out that it is very easy to forget how different BF machine is from a conventional computer with random access memory. This makes it easy to write code generation in wasteful style: the subconscious confidence that having more code than strictly necessary is not a problem because it could always be jumped over is very hard to beat. My compiler was a victim of my habit of working with computers which can jump over code: all functions were rather generic and would generate generic code for handling lots of situations in the runtime. This resulted in longer code, and longer code meant more steps needed to be taken to get around those pieces which were not supposed to be executed. It turned out that I had lots of code to remove and rearrange.
First of all I separated operations on operands having the same sign and reduced all operations on operands with potentially differing signs to a relatively short sign-processing block, then to an operation on operands with same sign followed by another sign postprocessing block. This shaved off about 10M steps, not too bad, but not fundamental enough.
Then I gave a stern look to all instances where I was adding a known constant to a cell, or setting a cell to constant value or doing something that originally involved creation of several temporary cells and replaced all straightforward high-level pieces of code with low-level direct manipulations. This saved me another 5M steps.
Looking closer I discovered a number of functions which used a lot of unnecessary allocations and sometimes inefficient algorithms (they also had a lot of TODOs in comments). Cleaning them all up and doing several more rounds of replacement of high-level generic operations with less generic special-purpose internal functions slowly shaved off another 15Msteps. Most wins were pretty small on the order of 0.5Msteps with a couple really large ones. For instance once I realized that I could simplify INTGT it saved me 3Msteps.
When I reached about 121Mstep I hit a wall. There was nothing left to tune, every round of optimization brought progressivley less improvement. As the last resort I tried shuffling FXP variables in memory. I ran a brute-force test which simply tried all permutations of variables to see if it is possible to achieve fewer steps, but the end result was less impressive than I hoped for. The best I could get was a bit less than 115Msteps. The majority of combinations resulted in rather small deviation from 121M. This test results could be seen on the image below:
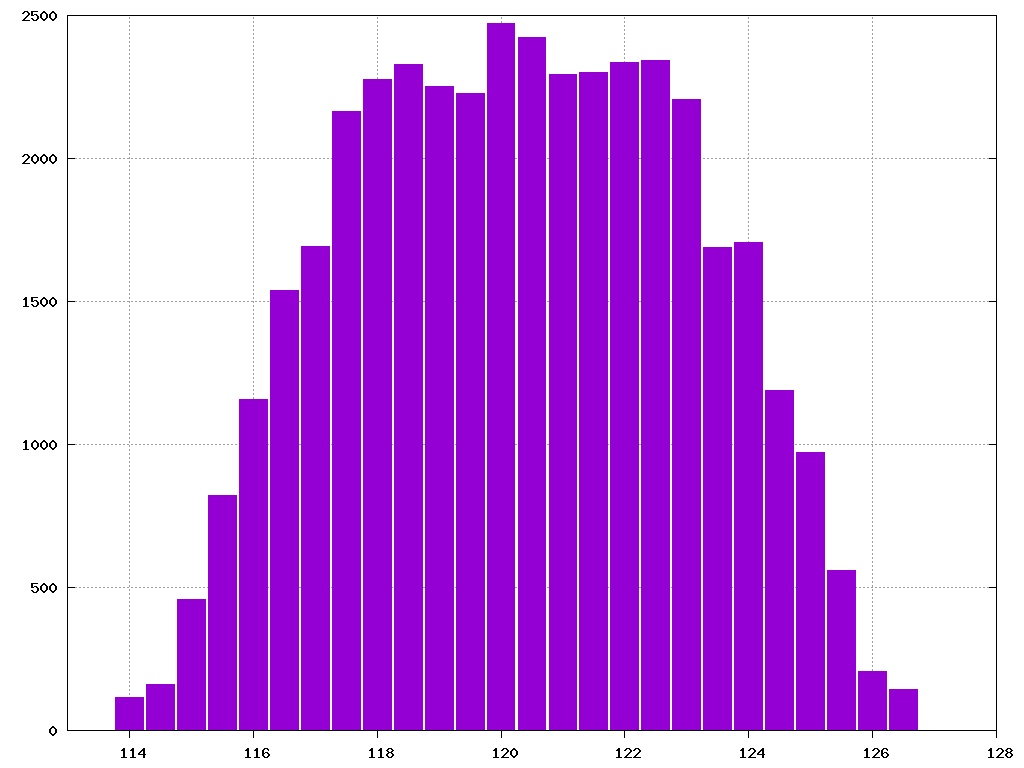
Number of variables combinations (y-axis) running for certain amount of megasteps (x-axis).
These results made perfect sense – the more often a variable was accessed the more effect its position relative to the area after variables allocation would affect time it took to do the access. Judging from this I concluded that in bigger programs with more variables the effect of variable shuffling would be diminished, especially if all variables were to be accessed equally often. I theorized that a more aggressive allocator, maybe one that would even dispose of unused user variables and add their space to scratch area could add some additional speedup, but it was unlikely that such speedup would be fundamental: it could never break the hard limit at around 90M imposed by the combination of chosen INT and FXP representations and BF peculiarities.
Ultimately the rigidity of my effectively non-existent type system proved to be a major optimization block. A lot of steps resulted from the need to modify full-sized FXP and INT values. Without an easy way of coercing numbers I could not meaningfully switch to shorter types even when I knew that they would be beneficial. I could have done that manually too, but that would have required more work than to implement a proper compiler. And would have been less fun as well, so I decided not to do that. My estimate was that it could have saved me another 20 to 30 Msteps.
One other idea I got while optimizing the compiler was to take the memory allocator and always pad INTs with, say, five cells, either before, or after them. My reasoning was like follows: INT operations require some temporary storage, this storage would contain data from arrays representing those INTs, so providing scratch holes between user variables could save an interpreter some time. I quickly checked this idea.
I was wrong again! It turned out, that any amount of holes would actually slow the code down, making it at times twice as slow as it were with the naive allocation. Apparently naive allocation was not so bad after all. Sure, it generated lots of temporary cells, but those cells would end up being allocated very close to each other. A quick brute force check of multiple padding values provided clear evidence that padding does indeed slow computations down. I decided to wait with allocator optimization until either an insight about typical access patterns of a generic compiled BF program or until I rewrote the compiler with proper parser and separation of concerns.
Summary and Lessons learned
Summary
- What happened: a compiler that is capable of producing code for simple computations was produced;
- What did not happen: there was no universal compiler which allows one to deal with arbitrary data structures; self-hosting goal was not achieved. Moreover, this goal proved to be reachable, but way too inefficient.
Lessons
- BF is very different from pretty much anything else;
- Not using proper parser is fine as long as the language is very primitive;
- Not using a parser for a language with more than one data type is painful;
- Not using a parser for a language which requires fine selection of primitives implementation is extremely painful;
- Decimal-digits integers are awesome. They also provide near constant time compared to native sized ones;
- Many algorithms which are good for random access memory are not so good when mindlessly ported to BF. I really wanted to benefit from Karatsuba, but ended up cooking some half-proven quick fixture which did not use too much code space;
- I had several ideas for speeding things up, but they all boiled down to replacing linear access with random access either via an external device or via a modification to internal representation of code (essentially having the interpreter work on run-length encoded version of code). Fun thing is that half of my hardware designs which are feasible rely on a device that converts a random access memory into a linear accessible one. The bottom line is BF should probably not be considered as a simple computational medium, even in the event of large-scale computation devices extinction, unless someone has access to robust, fast an cheap linear memory. One of my sketches employed some discrete logic glueing together several audio cassette decks. Unfortunately stock audio cassettes do not seem to be robust enough and would not tolerate frequent starts and stops. Maybe steel wire could do the trick. But from a practical stand point an easier solution is any model that allows jumps;
- While being a disaster for situations where computations involve large numbers this thing seems to be relatively usable for automating processes where values do not exceed the natural cell size;
- Self-hosing and indirect access is possible, but the most straightforward way to it is essentially writing an emulator of a computer with RAM in BF. This is feasible (see arrays), but would prove to be exceptionally slow;
- An improved sine code with just five variables instead of eight does not give much improvement – the best result for it is 111.5M vs 114.5M for a more straightforward version. This adds evidence to the limited contribution of data tape movements caused by variable access to the overall speed;
- Even with multiple data tapes movements removed it is still a problem that all counting is done one digit at a time (not even one bit!). This introduces the largest delay by far. Even an interpreter that can deal with rle-encoded code sine as defined above takes 75M steps to compute. While this translates to about two minutes of work of a reasonably feasible HW interpreter it is still too much and there is no way around it other than to introduce a copy instruction. Or even a multiply instruction and a multiplication table because every MxN operation takes KxMxN steps with K > 1.
In conclusion, this was a fun ride, unfortunately it turned out that BF is even less practical than I initially expected.
Here you can find the latest state of the “compiler”.
Suggested reading about proper compilers
As I have promised earlier here are some good books on compilers (in the order of how I recalled them):
-
Engineering a Compiler by Keith D. Cooper and Linda Torczon – thick, solid, has more knowledge packed than any casual reader might be looking for;
-
Crafting Interpreters by Robert Nystrom – not exactly about compilers, but bytecode VM section could be of interest (as well as the parsers parts);
-
Practical Compiler Construction by Nils M Holm – an interesting way of writing about compilers, rather terse, but occasionally illuminating;
-
Essentials of Compilation by Jeremy G. Siek – a rather compact introduction to the problem which relies on lots of excercises to convey ideas.