Rule 90 in Erlang: a Case Study
revision 1.0.0
Rule 90 for 1D cellular automaton produces a lovely Sierpinsky carpet when it starts with a single non-empty cell. It defines the next state of a cell in one dimensional cellular automaton as a XOR of current neighbors. It is trivial to implement in many styles and languages. While being extremely simple it provides a nice model for experiments with implementation of distributed systems in which nodes talk to neighbors through message passing. Here I’ll describe my small experiments with implementing it in Erlang and share what could be gleaned from it.
Reference Implementation
To make sure any experimental implementations produce correct results let’s cobble quick and dirty reference generator first:
-module(linlife).
-import(lists, [foreach/2, split/2, zip/2, filter/2, map/2]).
-export([go/0]).
-define(WIDTH, 25).
-define(NUMGEN, 15).
-define(DUP, lists:duplicate).
-define(PRINT, io:format).
go() ->
Field = ?DUP(?WIDTH div 2, false) ++ [true] ++ ?DUP(?WIDTH div 2, false),
make_step(Field, 1).
make_step(_, ?NUMGEN + 1) -> ok;
make_step(Field, Step) ->
show(Field, Step),
{B1, L1} = split(length(Field) - 1, Field),
{B2, L2} = split(1, Field),
Neighbors = zip(L1 ++ B1, L2 ++ B2),
make_step(map(fun({NL, NR}) -> NL xor NR end, Neighbors), Step + 1).
show(Field, Iteration) ->
?PRINT("~-4w ", [Iteration]),
foreach(fun(X) -> if X == true -> ?PRINT("H");
true -> ?PRINT(".") end end, Field),
?PRINT(" ~2w~n", [length(filter(fun(X) -> X end, Field))]).The code is rather straightforward: the only public function go() prepares a field of WIDTH cells with one cell in the middle set to true, others set to false and passes the ball to make_step(). The latter prints out the field, shifts the field left and right by one element and then loops after computing new field by applying XOR to shifted fields. As soon as a predefined number of steps is reached pattern (_, ?NUMGEN +1) matches and the loop finishes.
When run it will produce the following:
1 ............H............ 1
2 ...........H.H........... 2
3 ..........H...H.......... 2
4 .........H.H.H.H......... 4
5 ........H.......H........ 2
6 .......H.H.....H.H....... 4
7 ......H...H...H...H...... 4
8 .....H.H.H.H.H.H.H.H..... 8
9 ....H...............H.... 2
10 ...H.H.............H.H... 4
11 ..H...H...........H...H.. 4
12 .H.H.H.H.........H.H.H.H. 8
13 H.......H.......H.......H 4
14 HH.....H.H.....H.H.....HH 8
15 .HH...H...H...H...H...HH. 8A piece of Sierpinsky carpet with an addition of generation number and the number of alive cells in each generation. It takes about 8 ms to print the image above of which most is spent on formatting and printing out the image with actual computation taking less then 250 us. It takes ~60.5 ms to compute 15k generation with this approach. I like to measure things so below is a table with computation time as function of world size and number of generations.
Cell No 10 100 1000
17 4.2e-5 2.81e-4 0.00271
33 5.3e-5 4.73e-4 0.004614
65 9.8e-5 8.75e-4 0.008727
129 1.71e-4 0.001609 0.016249
257 3.52e-4 0.003294 0.03296
513 7.84e-4 0.00668 0.065937
1025 0.001502 0.012434 0.124597
2049 0.002826 0.025358 0.255067
4097 0.005658 0.05185 0.542044
8193 0.012276 0.107905 1.067854The table basically tells us that the more cells are processed for bigger periods the longer it will take it to compute with time growing pretty linearly.
Apart from showing samples of slightly unusual syntax the code is very straightforward and does not allow Erlang to shine in all its glory. (A note for erudites, yes, it could be done using bitstrings, yes, it will be much much faster than lists, but no, I am not using it as a reference point since the looks of resulting code will provide too much of a distraction for no gain.) Let us consider a different approach to see what else Erlang could offer.
Cellular Automata Revisited
One dimensional cellular automaton is extremely simple so it is very tempting to consider it as an array and to perform array operations on it. Let’s consider instead what was used as an inspiration for cellular automata: cells. Cells are autonomous objects which occupy some space, exchange chemicals with the outside world through the border of this space and change their state basing on what has been received. In the reduced world of one dimensional cellular automaton cells emit not signalling molecules but their state to neighbors and receive states from the neighbors. Basing on current state and neighbors’ states the next state is computed. In case of rule 90 self state is irrelevant and the next state is just a XOR of neighbor states.
In terms of Erlang each cell could be represented with a process which is responsible for receiving messages with updates from neighbors, computing next state and emitting updates to all interested parties – neighbor cells and possibly some monitoring process used for displaying global state. Obviously such process should remember who are its neighbors and supervising process. When running it must keep track of who has already sent an update. Thus internal state processing could look like this:
cell_process(PID, State, Info) ->
NewNeighborState = Info#cellinfo.neighborstates ++ [State],
NewWaitList = delete(PID, Info#cellinfo.waitonlist),
[NextNeighbor] = delete(PID, Info#cellinfo.neighborpids),
if NewWaitList == [] ->
NewState = compute_next_state(NewNeighborState),
foreach(fun(X) -> X ! {self(), stateupdate, NewState} end,
Info#cellinfo.neighborpids),
Info#cellinfo.superpid ! {self(), NewState},
NewInfo = Info#cellinfo{selfstate=NewState,
neighborstates=[],
waitonlist=Info#cellinfo.neighborpids};
true ->
NewInfo = Info#cellinfo{neighborstates=NewNeighborState,
waitonlist=NewWaitList}
end,
{NextNeighbor, NewInfo}.
compute_next_state(NeighborStates) ->
foldl(fun(X, A) -> X xor A end, false, NeighborStates).Internal processor gets PID of a neighbor and neighbors’ state as an input. In order to try to preserve purity internal state is carried around as another argument which could be a record defined as follows:
-record(cellinfo, {superpid :: identifier(), % PID of a supervisor
selfstate :: boolean(),
neighborpids :: [identifier()],
neighborstates = [] :: [boolean()],
% These cells have not sent an update yet:
waitonlist :: [identifier()]}).After neighbor state list is updated and current neighbor’s PID is removed from a list of not reported members the next neighbor to wait on is determined. This is an important step to perform but more on it later, for now let’s just remember that it has been done. The following code is rather clear as well: if every neighbor has reported then compute new self state, send messages with the new state to supervisor and to each neighbor, clean up neighbor states list and populate wait list with all members’ pids. If, however, not everyone has reported yet, then just update state record. The last statement just returns a tuple of next PID to wait on and new inner state. It is worth noting that decoupling of rule logic from bookkeeping happens rather naturally here and to switch to two dimensional cellular automaton by slightly modifying cellinfo record and by supplying proper compute_next_state().
All is well, but who initiates processing, i.e. who calls cell_process()? It turns out that one must define several helper functions to set everything up. General logic is this: first some initial process gets spawned with some initialization function which passes the ball to main code which loops as long as it receives messages it can understand, parses them and, in turn, calls the processor. The code implementing it is preset below as well as discussion:
cell(SupervisorPID) when is_pid(SupervisorPID) ->
SupervisorPID ! {self(), online},
receive
{SupervisorPID, init, InData} ->
foreach(fun(X) ->
X ! {self(), stateupdate, InData#initializer.state} end,
InData#initializer.neighbors),
Info = #cellinfo{superpid=SupervisorPID,
selfstate=InData#initializer.state,
neighborpids=InData#initializer.neighbors,
neighborstates=[],
waitonlist=InData#initializer.neighbors}
end,
cell(Info);
cell(Info) ->
receive
{PID, stateupdate, State} ->
{NextNeighbor, NewInfo} = cell_process(PID, State, Info);
stop -> NextNeighbor = 0, NewInfo = 0, exit()
end,
cell(NextNeighbor, NewInfo).
cell(PIDToWait, Info) ->
receive
{PIDToWait, stateupdate, State} ->
{NextNeighbor, NewInfo} = cell_process(PIDToWait, State, Info);
stop -> NextNeighbor = 0, NewInfo = 0, exit("Bye!")
end,
cell(NextNeighbor, NewInfo).For each cell supervising process (which will get a bit of attention later) spawns cell() and passes it its PID. First thing the fresh cell does is to ping supervisor back and tell it that it has successfully spawned. Then it waits till supervisor provides it with details about its desired state and PIDs of its neighbors. As soon as supervisor provides it with initialization data it messages neighbors. This initialization scheme might look complicated, but in fact it is not – it actually reduces the amount of work a supervisor must do (it does not need to do some fancy preallocation to init cells immediately). After a cell has performed this initialization stage it moves to the second one which turned out to be important. Now a fresh cell is waiting for its first update from a neighbor. Since all processes are running asynchronously we can’t generally be sure who sends this update first, so the cell does not make any expectations and just waits for an update. However as soon as first update message is received the cell morphs one last time and now it is waiting for an update from a very specific neighbor, i.e. the one who was not the first. And this is very important since as we can’t predict which process finishes computing its next state first, we can’t guarantee that a cell won’t get two updates from the same neighbor in a row which, in turn, could trigger a false state update! That’s why cell_process() returns NextNeighbor – we should explicitly wait on it or the results might get funny. What is even more funny, one would occasionally get correct results, just because it happened so that the processes were scheduled in favorable order. I tried running the code without this last morph and managed to get expected results in whooping forty four runs out of two thousands. If nothing else this must convince anyone that adding a little of local synchronicity could be rather helpful. (Now one might wonder what happens if some process still manages to send several messages before its peers. Good news – nothing disastorous! The messages won’t be procecced, but as long as the cell is alive they will stay in process’ messagebox, so the next time process actually waits for updates from this particular speedy peer it will immediately get those in exactly the same order they were received.) Now the cell is looping endlessly as long as nobody is sending it atom ‘stop’.
One piece is still left out – supervisor process which orchestrates cells. Basing on the experience with cell process it is easy to guess that it could be constructed as a succession of functions responsible for different initialization steps. Recalling stages of a single cell it is easy to come up with what has to be done:
- spawn all cells;
- wait for all cells to report their online status;
- initialize running cells;
- collect cell states;
- when enough generations have reported back shut everything down.
The corresponding code might look like following:
-module(life).
-export([run/2]).
-import(lists, [foreach/2, member/2, delete/2, foldl/3, keyreplace/4,
seq/2, map/2, keyfind/3, sublist/2, filter/2]).
-record(cellinfo, {superpid :: identifier(),
selfstate :: boolean(),
neighborpids :: [identifier()],
neighborstates = [] :: [boolean()],
waitonlist :: [identifier()]}).
-record(initializer, {state :: boolean(),
neighbors :: [identifier()]}).
run(NumCell, NumGen) ->
run(NumCell, [], NumCell, NumGen).
run(Num, CellMap, NumCells, NGen) when Num >= 0 ->
NewCell = spawn(cell, cell, [self()]),
run(Num-1, [{Num, NewCell}] ++ CellMap, NumCells, NGen);
run(_, CellMap, NumCells, NGen) -> waitonline(CellMap, 0, NumCells, NGen).
waitonline(WhomToWait, Ctr, NCells, NGen) when Ctr < NCells ->
receive {_, online} -> waitonline(WhomToWait, Ctr + 1, NCells, NGen) end;
waitonline(CellList, Ctr, NCells, NGen) ->
UpdatePairs = map(fun(X) -> get_neighb_pids(X, CellList, NCells) end,
CellList),
init_cells(UpdatePairs, [], NCells, NGen).
init_cells([], StateMap, NCell, NGen) ->
cell_monitor(StateMap, 0, TStart, NCell, NGen);
init_cells([NextCell | RemainingCells], StateMap, NCell, NGen) ->
{Num, PID, Neighbors} = NextCell,
if Num == NCell div 2 -> State = true;
true -> State = false
end,
PID ! {self(), init, #initializer{state=State, neighbors=Neighbors}},
init_cells(RemainingCells, [{Num, PID, [State]}] ++ StateMap, NCell, NGen).
cell_monitor(FieldState, Num, TS, NCell, NGen) when Num < NCell*NGen ->
receive _ -> ok end,
cell_monitor(FieldState, Num + 1, TS, NCell, NGen);
cell_monitor(FieldState, _, TS, NCell, NGen) ->
foreach(fun(X) -> {_, PID, _} = X, PID ! stop end, FieldState).Here the code ended up to be rather trivial as well: run() spawns the requested number of cells, then calls waitonline(). waitonline() just counts how many times it was told that a cell is online and as soon as it was updated as many times as there are cells it invokes init_cells() which, unsurprisingly, tells each cell who its’ neighbors are and what its’ current state is. When done it passes the ball to cell monitor.
A careful reader should have asked by now “Why cell monitor does essentially nothing with state updates it receives? Also why there is a wildcard in pattern?”. Well, to answer the second one – the system under consideration is rather simple and I decided that it is ok to cut a few corners this particular time. As to why state updates are ignored, it turned out that writing decent real-time state displaying code was taking me much more time than implementing everything else, so I’ve shortcutted a bit and cobbled a Python script listening to a socket and doing all the formatting and printing. It is trivial, does not add any value to the discusison and I decided not include it.
Now it is time to fire up the code and see what happens. Run results could be seen in the table below:
Cell No 10 100 1000
17 3.97e-4 0.00587 0.03288
33 0.001712 0.010163 0.058069
65 0.001415 0.013891 0.099306
129 0.00516 0.026559 0.197915
257 0.009532 0.048242 0.407558
513 0.016565 0.091794 0.936569
1025 0.022423 0.202998 2.054239
2049 0.058971 0.512124 4.535901
4097 0.207364 1.794758 10.411121
8193 0.675303 2.871532 27.610455It could already be clearly seen that it takes significantly longer to do computations for any population size now than when ordinary lists were used. The reason is easy to guess: no matter how lightweight cell processes have to be scheduled and switched, messages have to be sent, all necessary maintenance must be done, and all these small costs eventually sum up to significantly slow the automaton down. “But if it slows everything down so much what is the point of this implementation?” one could justly ask. Bear with me a little more and it will become eventually clear.
Going Multinode
Consider what happens if you have to compute a fixed number of generations in a certain amount of time. If you are using the first implementation you are fine as long as your population size is below some threshold value which is determined by hardware you use. But what are you options when you hit this threshold after you absolutely must increase population size? You could try running your load on better hardware, you could try tweaking your operting system settings to make it disturb your program as little as possible, but all these options are rather limited. There is not much to do when they are depleted and you still have to add some more cells. Somewhat surprisingly the slow implementation can show a path to salvation.
Recall that each cell is a process now. A process communicates with other processes through their IDs. It turns out, that it does not really matter whether a process is running in the same VM, in a different VM on another core or somewhere in a network as long as the VM it is running on is connected to other VMs and its ID is known. So the cell process will stay the same no matter where on Earth its peer is, and it is not an exacerbation, since a peer process could indeed physically exist on the other side of the planet as long as network latency does not matter.
The only place a change must be introduced is the supervisor. Now it must take into consideration the distribution of cells across nodes. In this study I’ll assume static nodenames, static naming scheme and static connections between nodes which could be not the case in real world scenarios. These assumptions will, as usual, won’t overload the resulting code and won’t shadow the important parts. I will have to introduce a bunch of hardcoded values, which I belive is totally fine for a synthetic study.
Before diving deep into changes to supervisor let me first describe test setup.
Now I will run the code on two Erlang VMs, one running a supervisor and started
as erl -sname thranduil on physical host named ‘mirkwood’, another named
‘elrond’ and running on a host named ‘rivendell’. I’ll hardcode these names for
the sake of simplicity. Both hosts must be able to reach each other, be able to
resolve each other’s names and share code. For a quick test all these
prerequisites could be easily satisfied manually, however please don’t forget
that any real-world application would require proper automation. The nodes are
true hardware ones because I’ve decided against running multiple virtual nodes
in order to reduce possible measurement noise. In this setup ‘elrond’ does
nothing while life:run() is called on ‘thranduil’. Now to the code changes.
First of all, two VMs must find out about each others’ existence. Cheapish way to help them is to make one ping another. It is convenient to do it first when running the code:
run() ->
pong = net_adm:ping('elrond@rivendell'),
...Now if ‘elrond’ is reachable on ‘rivendell’ and it returns ‘pong’ the code will continue to execute in exactly the same manner as before. The other issue to resolve is how to start cells remotely. It turns out, that this could be done easily by using spawn/4 which takes a node on which to run a function as an argument. Now since I have only two nodes at hand I’ll just split cells array in two and run one half on one node, and other one on another. The code for doing so turned out trivial as well:
run(CellCtr, CellMap, NumCells, NGen) when CellCtr >= 0 ->
if CellCtr > (NumCells div 2) -> Node = node();
true -> Node = 'elrond@rivendell'
end,
NewCell = spawn(Node, cell, cell, [self()]),
...And that’s it. Apart from additional work of setting up two servers all that has to be done to distribute the load over them could be boiled down to those five lines above. While this is really not the best way to approach load distribution it is still capable to give some feeling of the amount of work needed. As a mental exercise consider how the same task could be done with your language of choice.
With code written and nodes ready it is time to run measurements! Here are the run results:
Cell No 10 100 1000
17 0.029516 0.312973 6.528962
33 0.035309 0.293366 4.599328
65 0.019603 0.266519 2.888129
129 0.016427 0.300707 22.978286
257 0.011035 1.815778 59.821181
....................... wait, what?!Which unambigously tell us that connecting two nodes via a wireless network was a very bad idea. Anyway, I had to try it to see what would happen. Now let’s connect the nodes with good old wires and see if the times improve:
Cell No 10 100 1000
17 0.006196 0.045763 0.40451
33 0.01086 0.066265 0.455357
65 0.003999 0.064106 0.646815
129 0.005138 0.071591 0.612606
257 0.006841 0.090289 0.873023
513 0.010659 0.112242 1.319318
1025 0.018277 0.17078 2.197606
2049 0.038378 0.366629 4.20114
4097 0.073783 0.914429 8.553961
8193 0.185747 3.045522 16.233432Now it looks more like something one would expect to see: it takes less time to do the job on two nodes than on one. For the convenience of analysis I am including a plot of distributed run compared to fully local run and naive expectation of two-fold speedup:
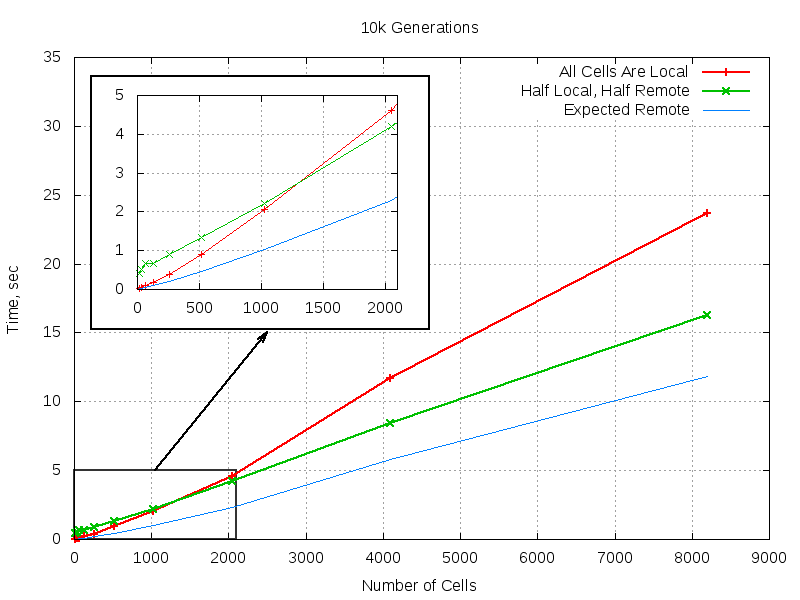
These results meet expectations: there is obviously a network overhead that is especally visible on small populations which plays smaller and smaller role on bigger ones and which eventully gives way to speedup. The speedup is not as big as one could hope for – around 1.5 instead of maximal 2, but it is still clearly visible. It would have been nice to try spreading the load over more nodes, but it turned out that all I could procure in reasonable amount of time were just two nodes with LAN port, so larger clusters will have to wait till I lay my hands on more computers with a socket for twisted pair. The code turned out to be rather trivial and compact. Of course it is not robust enough and lots ad lots of possible corner cases related to sudden deaths of cells are not covered, but it is not the purpose of a POC to deal with corner cases. It should serve an illustrative purpose which I hope it does well. Also it hints on another path for improving performance: one could combine the best of two implementations, the speed of list based and scalability of process based by introducing processes dealing with groups of cells.
Conclusion
This small study had a simple goal – to showcase a way of reasoning about distributed systems in terms of Erlang, a tool designed specifically to tackle essentially concurrent systems and streams of events. Note, however, that demonstrated way is by no means the best one to use Erlang, but a mere primer, aimed mostly to wet appetite and hint on what could be done. Many aspects crucial to real world systems were left out: proper supervision, OTP and others. I decided that those were not really important for a simple study like this and would obscure the benefits of Erlang rather than highlight them. All in all it is a complex tool which requires certain effort to master. Also I hope that I have not created any false expectations, since being a good tool for a specific task set does not make it a silver bullet (which, unfortunately does not seem to exist). While almost any task could be solved by using Erlang it is better not to forget that the same holds true for a really fast Brainfuck interpreter, so understanding when not to use something is no less important.
Afterparty
As a postscriptum I decided to share a bitstring implementation without further discussion:
-module(bitlife).
-export([run/2]).
-define(OUTPUT(Y),
io:format("~s~n", [[case X of $0->$.; $1->$H end ||
X <- lists:flatten(io_lib:format("~33.2.0B",
[Y]))]])).
run(NCell, NGen) ->
HS = NCell div 2,
BS = NCell + 1,
<< InitField:BS >> = << 0:HS, 1:1, 0:HS >>,
?OUTPUT(InitField),
step(InitField, NCell, NGen),
step(_, _, 0) -> ok;
step(Field, NCell, Ctr) ->
BS = NCell + 1,
<< First:1, Rest:NCell >> = << Field:BS >>,
<< Begin:NCell, End:1 >> = << Field:BS >>,
<< LS:BS >> = << Rest:NCell, First: 1 >>,
<< RS:BS >> = << End:1, Begin: NCell >>,
<< NewField:BS >> = << (LS bxor RS):BS >>,
?OUTPUT(NewField),
step(NewField, NCell, Ctr - 1).It is blindingly fast compared to any of presented implementations and also looks rather alien to the first look. Despite the looks it might be worth using keeping this option in mind.
Cell No 10 100 1000
16 1.5e-5 9.2e-5 8.96e-4
32 1.2e-5 9.0e-5 8.87e-4
64 1.5e-5 1.32e-4 0.001243
128 2.2e-5 1.68e-4 0.001627
256 2.5e-5 2.07e-4 0.002041
512 5.0e-5 4.26e-4 0.004243
1024 6.9e-5 5.97e-4 0.006045
2048 1.12e-4 9.49e-4 0.009607
4096 1.63e-4 0.001566 0.015906
8192 2.86e-4 0.002798 0.02803Another interesting observation happened when I tried to increase array size on two physical nodes some more. Instead of speedup I got significant slowdown and a nasty memory leak, but that is a core of a different story.